Following on from the last post discussing the use of mathematics within Building Management Systems Explained, the question of mathematics of control loop response analysis has been asked. This mathematics centres around the following techniques to help you understand how well a loop is tuned:
- Integral of Absolute Error
- Integral of Square Error
- Integral of Time-Weighted Absolute Value of Error
- Integral of Time-Weighted Error Squared
The best approach to discuss these techniques is to provide a pseudo code example of how these calculations can be carried out. Before I create this code I need to speak to absolute values.
The absolute value is the non-negative value without regard for the sign. |Value| is defined as the absolute value. Therefore, if Value is a negative number, |Value| is always a positive number.
I will show an example of how to calculate the Integral of Absolute Error and pseudo code for the other three integral methods. From the initial example and pseudo code of other methods, you should be able to calculate these values for your own data sets.
Integral of Absolute Error
Integral of Absolute Error, or IAE, is calculated as follows:
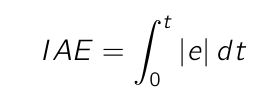
The pseudo code to calculate the Integral of Absolute Error is as follows:
Set a Counter to iterate from the second position to the last position.
|Previous Error| = Previous Process Variable – Previous Setpoint
|Current Error| = Current Process variable – Current Setpoint
Time Difference = Time of Current Error – Time of Previous Error
IAE = IAE + (Time Difference/2)•(|Previous Error| +|Current Error|)
Iterate CounterIn reality how does this pseudo code operate? Let us look at an example:
| Time | 1 | 2 | 3 | 4 | 5 |
| Setpoint | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| Process Variable | 21.5 | 21.0 | 19.5 | 19.0 | 19.5 |
On the first pass the following is the output:
Counter = 2
|Previous Error| = |21.5 – 20.0| = 1.5
|Current Error| = |21.0 – 20.0| = 1.0
Time Difference = 2 – 1 = 1
IAE = 0 + (1/2)•(1.5 + 1.0) = 1.25
Counter = Counter + 1 = 2 + 1 = 3| Time | 1 | 2 | 3 | 4 | 5 |
| Setpoint | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| Process Variable | 21.5 | 21.0 | 19.5 | 19.0 | 19.5 |
| IAE | 0 | 1.25 |
On the second pass the following is the output:
Counter = 3
|Previous Error| = |21.0 – 20.0| = 1.0
|Current Error| = |19.5 – 20.0| = 0.5
Time Difference = 3 – 2 = 1
IAE = 1.25 + (1/2)•(1.0 + 0.5) = 2
Counter = Counter + 1 = 3 + 1 = 4| Time | 1 | 2 | 3 | 4 | 5 |
| Setpoint | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| Process Variable | 21.5 | 21.0 | 19.5 | 19.0 | 19.5 |
| IAE | 0 | 1.25 | 2 |
On the third pass the following is the output:
Counter = 4
|Previous Error| = |19.5 – 20.0| = 0.5
|Current Error| = |19.0 – 20.0| = 1.0
Time Difference = 4 – 3 = 1
IAE = 2 + (1/2)•(1.0 + 0.5) = 2.75
Counter = Counter + 1 = 4 + 1 = 5| Time | 1 | 2 | 3 | 4 | 5 |
| Setpoint | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| Process Variable | 21.5 | 21.0 | 19.5 | 19.0 | 19.5 |
| IAE | 0 | 1.25 | 2 | 2.75 |
On the final pass the following is the output:
Counter = 5
|Previous Error| = |19.0 – 20.0| = 1.0
|Current Error| = |19.5 – 20.0| = 0.5
Time Difference = 5 – 4 = 1
IAE = 2.75 + (1/2)•(1.0 + 0.5) = 3.5 | Time | 1 | 2 | 3 | 4 | 5 |
| Setpoint | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| Process Variable | 21.5 | 21.0 | 19.5 | 19.0 | 19.5 |
| IAE | 0 | 1.25 | 2 | 2.75 | 3.5 |
Integral of Square Error
Integral of Square Error, or ISE, is calculated as follows:
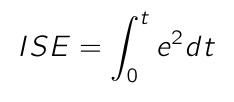
The pseudo code to calculate the Integral of Square Error is as follows:
Set a Counter to iterate from the second position to the last position.
|Previous Error| = Previous Process Variable – Previous Setpoint
|Current Error| = Current Process variable – Current Setpoint
Time Difference = Time of Current Error – Time of Previous Error
ISE = ISE + (Time Difference/2)•(square(|Previous Error|) +
square(|Current Error|))
Iterate CounterIntegral of Time-Weighted Absolute Value of Error
Integral of Time-Weighted Absolute Value of Error, or ITAE, is calculated as follows:
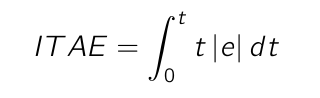
The pseudo code to calculate the Integral of Time-Weighted Absolute Value of Error is as follows:
Set a Counter to iterate from the second position to the last position.
|Previous Error| = Previous Process Variable – Previous Setpoint
|Current Error| = Current Process variable – Current Setpoint
Time Difference = Time of Current Error – Time of Previous Error
Time Since Start = Time of Current Error – Time of Since Start
ITAE = ITAE + (Time Difference/2)•(Time Since Start•|Previous Error|
+ Time Since Start•|Current Error|)
Iterate CounterIntegral of Time-Weighted Error Squared
Integral of Time-Weighted Error Squared, or ITSE, is calculated as follows:
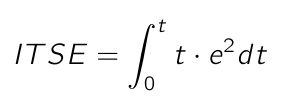
The pseudo code to calculate the Integral of Time-Weighted Error Squared is as follows:
Set a Counter to iterate from the second position to the last position.
|Previous Error| = Previous Process Variable – Previous Setpoint
|Current Error| = Current Process variable – Current Setpoint
Time Difference = Time of Current Error – Time of Previous Error
Time Since Start = Time of Current Error – Time of Since Start
ITSE = ISTE +
(Time Difference/2)•(Time Since Start•square(|Previous Error|)
+ Time Since Start•square(|Current Error|))
Iterate Counter